Not so simple: The simple redirected winch pull

Take any reasonably comprehensive winching course and, once you’ve covered the basic single-line pull, you’ll be introduced to the snatch block—or, more recently, its elegant one-piece alternative, the billet-aluminum recovery ring.

A pulley—which is what both devices are—serves a couple of purposes in a winch system. Most impressively, when a winch line from a vehicle is led through a pulley attached to an anchor and then back to a recovery point on the vehicle, the power of the winch is essentially doubled (minus minor frictional losses) while line speed is halved. (A corollary to this is that by pulling more line off the winch to rig a double-line pull, you are further increasing the power of the winch by reducing the layers of line on the drum. Thus you receive a double benefit during a difficult recovery.)

The other valuable use of a pulley is to redirect a pull—around a corner as it were—when a straight one is either awkward, dangerous, or impossible. It’s frequently used to recover a bogged vehicle when a recovery vehicle equipped with a winch cannot be positioned directly in front of it. A suitable anchor such as a tree is employed as a redirect point, using a tree strap and a pulley.

When you learn how to rig a redirected pull you’ll also learn that this use of a pulley does not multiply the power of the winch, nor does it halve the line speed. The easiest way to figure out whether or not you are multiplying winch power in any situation is to count how many lines are shortening when you engage the winch. For example, in the illustration below labelled Double-line Pull, both the line from the winch to the pulley and the line from the pulley back to the vehicle will shorten as the winch pulls, thus the power is multiplied by two.

On the other hand, in our simple redirected-pull scenario above, only the line running from the pulley to the bogged vehicle will shorten—the distance between the pulley and the winching vehicle will not change. Therefore the winch is operating at its rated power.

But now comes the not-so-simple  part. What about the load on the anchor?

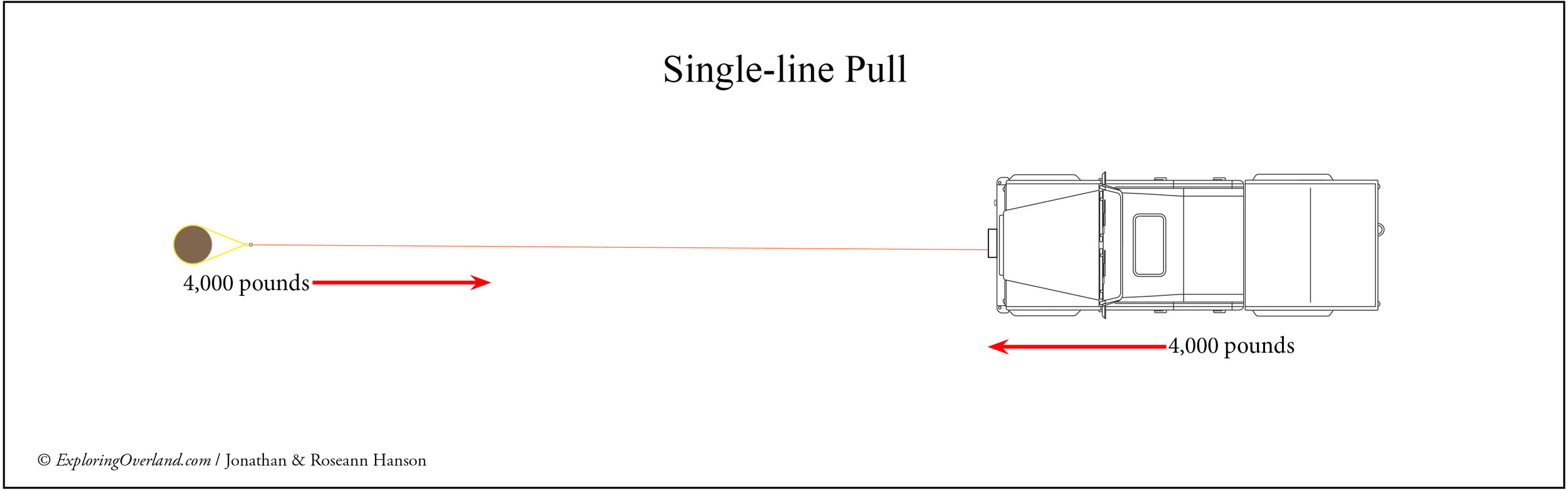
Let’s assume that in all our scenarios, the bogged vehicle needs 4,000 pounds of pull to retrieve it. If the operator rigs a single line pull to the tree anchor directly in front of the vehicle and engages the winch, the load on both the winch and the tree is 4,000 pounds.

If the operator rigs a double-line pull, the vehicle still needs only 4,000 pounds of pull to move. Due to the effects of the pulley the load on each line is halved, to 2,000 pounds; thus the winch is  only exerting 2,000 pounds (and only drawing the amperage necessary for that), and the recovery point on the vehicle is also experiencing 2,000 pounds of force. The load on the anchor remains 4,000 pounds.

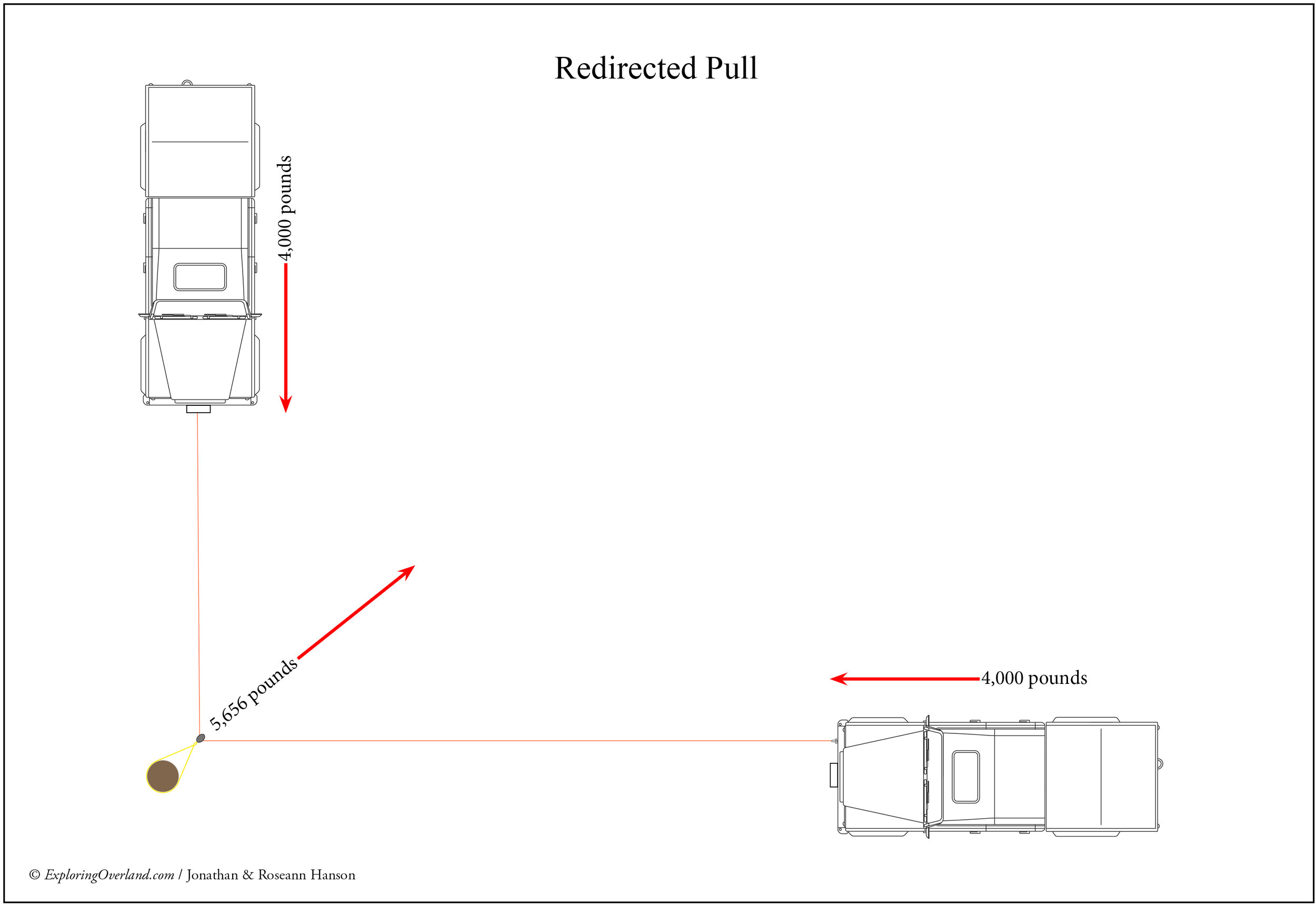
So far so good. Now let’s take another look at our redirected pull, where one vehicle is at 90 degrees to the other. In this scenario, the bogged vehicle still needs 4,000 pounds of force to move. The winch on the recovery vehicle is also subjected to 4,000 pounds—again taking into account slight frictional losses. So the force on the anchor must also be 4,000 pounds, right?

Actually . . . no.

In this case—a 90-degree redirected pull—the force on the anchor will actually be 5,656 pounds, almost 50 percent higher. The force is calculated using the formula:

pull = 2t(cosine x)

 . . . where pull is the force on the anchor, t is the force exerted by the winch, and x is one half the angle at which the winch line passes through the pulley (in other words, the direction in which the anchor would move if it failed; in a 90-degree redirect it would be 45 degrees).

So, in our case, 2 x 4,000 pounds is 8,000, multiplied by the cosine of 45º which is .707, equals 5,656 pounds. 

There’s more. As the angle between the bogged vehicle and the recovery vehicle narrows, the force on the anchor continues to increase. Imagine the scenario below, in which the recovery vehicle has to be situated directly alongside the bogged one—I’ve been in this situation. In this case, with the angle between the winch lines near zero, the force on the anchor would be (very nearly) doubled, to 8,000 pounds—even though the bogged vehicle is still only subject to 4,000 pounds of pull to free it. Imagine a tougher scenario in which the recovered vehicle took the full might of, say, a 10,000-pound winch to free it. In such a case that pine tree you wrapped your strap around is going to have about 20,000 pounds of force trying to pull it over—and all the hardware attached to it will be subject to the same stress.

You don’t actually have to have a calculator with a cosine function to figure the increase in force if you use a chart such as this, where “factor” equals how much the force on an anchor is multiplied by different angles of redirected pull :

And, in reality, you don’t need to do any figuring or checking at all. All you need to remember is that in any redirected pull, the force on the anchor can be up to twice what the rest of the system is subjected to. And the anchor includes the tree or chocked vehicle or whatever you are rigging to, as well as the tree strap, shackle, and pulley in the anchor assembly.

Non-instinctive effects of physics such as this reinforce the axiom always to use recovery equipment rated for the vehicle and winch, with working load limits (WLL) clearly marked, and adequate safety factors.